What is an algorithm ?

Nowadays, algorithms are everywhere, cities are « connected », there is the Internet of Things – IoT -, everyone use algorithms without knowing it. When we speak about algorithms and artificial intelligence, we think to movies such as IRobot, Terminator or The Space Odyssey where the machine is a thinking being and take over the planet. In 2019, Google launched AlphaStar, an AI playing StarCraft2. Alphastar can beat the world best StarCraft2 players. IBM developed Watson, an AI who can process natural language – NLP -. In 2011 Watson competed on Jeopardy! against the two champions, winning the first place.

So what is an algorithm ? Is it a recipe ? Yes it is, but I am not going to use this example. I prefer to explain it through another example. After giving the definition with an example, we will see what are the algorithms’ limitations.

For the slides in french you can click here.

Algorithm by example

Do you know what a maze is ? It is a simple game, there is one entrance and one exit. The goal is to find the exit. This maze has been created by Prim’s algorithm.

• 

• 

Several strategies can be used to find the solution however let’s change the point of view. Currently we can see the whole maze, hence we know where we are. If it was a real size maze, you would only see walls around you and you would have no way to see the whole maze hence your position in it. It would be easy to be lost and turn round and round even to walk through a path you already walked by.

Do you know that there is an algorithm to find the exit ? Could you figure out this algorithm with all the following instructions ?

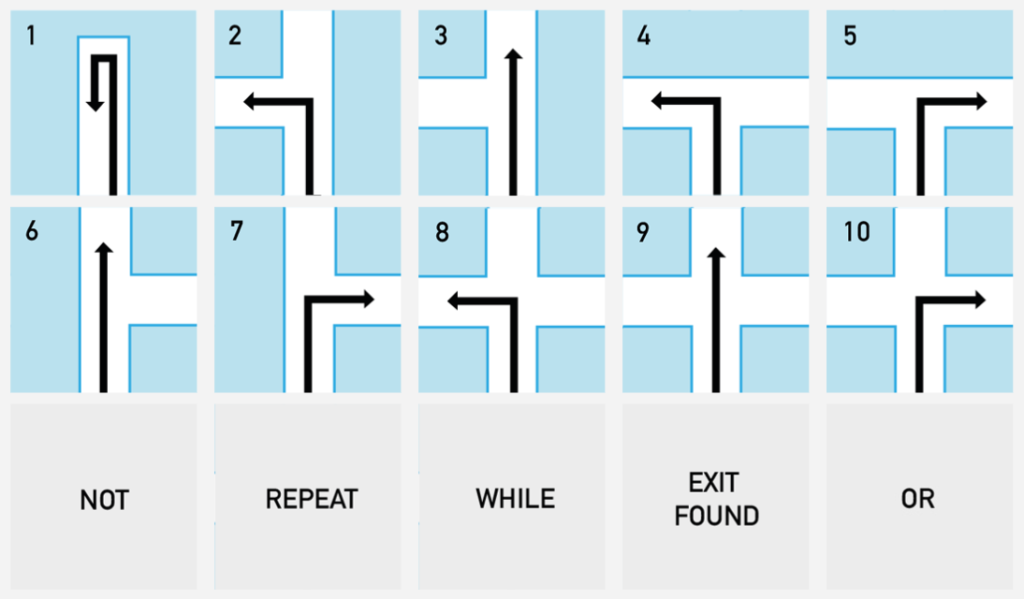
As you can see, these « instructions » cover all the possible cases. For each case you can choose one action.

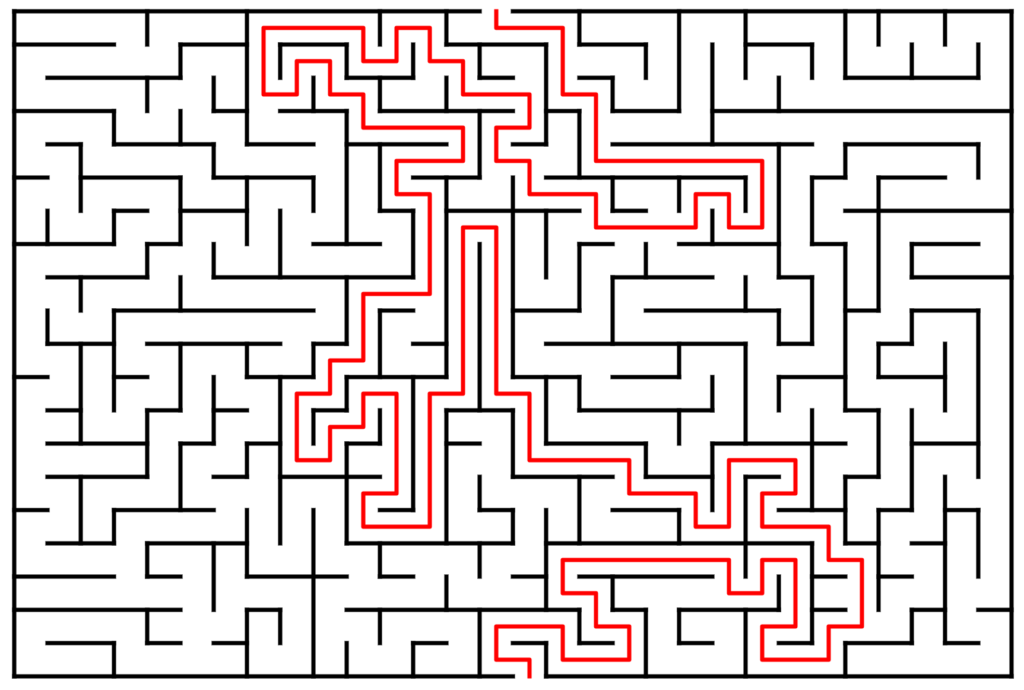
Here is the solution:

First go straight on. // enter in the maze
For any crossing, go left.

With the icons, it is:

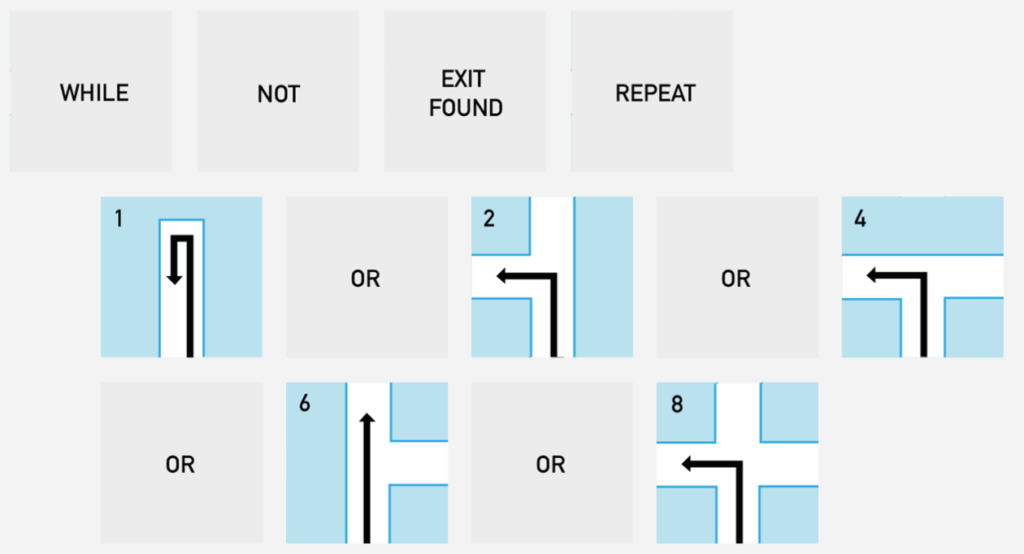
You can think that it is not a piece of code because you can read it and understand it without having studied computer science. You might be a bit right, in computer science we call that « pseudo code ». It is the code, but only the high logic, we don’t want to bother with the implementation details, we only want to keep the logic.

Question: Could we switch the two instructions ? We would get:

For any crossing, go left.
First go straight on. // enter in the maze

It does not make any sense. Indeed, order matters !

Question: Could remove the word « left » from the last sentence ? We would get:

First go straight on. // enter in the maze
For any crossing, go.

Once again, it does not make any sense ! Instruction must be accurate.

You can notice that there is a finite number of instructions.

Now you should start to understand that a algorithm is a finite set of ordered and accurate instructions.

Let’s introduce a more formal definition of an algorithm:

In Computer Science an algorithm is a finite sequence of well defined, computer implementable instructions to solve a class of problems.

An algorithm is a program – a piece of code – and this program must finds the solution to a given problem but not any piece of code is an algorithm.

It is very important to understand that an algorithm always finds a correct solution to a given problem otherwise, it is not an algorithm, it is just a program.

For many problems any solution can be good but for other problems the optimal solution is what we are looking for. For the first set of problems the question is: « is there a solution? », and for the other set of problems the question is: « what is the optimal solution? », in this case, most of the time it is fairly easy to get any not optimal solution and then we try to improve it.

Furthermore not all problems can be solved by an algorithm.

Age of the captain

It is possible to create an algorithm to answer this question : « If a ship has 26 sheep and 10 goats, how old is the captain ? » ?

The answer is no. Not all problems have a solution. It misses inputs. To be solved a problem must be well defined. All the necessary inputs to solve the problem must be provided.

The barber paradox

A barber is very particular, he shaves every person who does not shave themselves and no ones who shave themselves.

Question: Does the barber shave himself ?

You can see the contradiction. Such a barber can’t exist.

This problem is not « decidable » so there is no way anyone could create an algorithm to answer this question.

Is it really a computer science problem ? Yes, we can try to solve this kind of logic problem with boolean logic and a SAT-solver.

A time and travel problem

This time, there is no time problem but a problem because of the time.

We are going to talk about a class of problems that are very hard, let’s call them: the « very very very very very very hard » problems or the NP-hard problems, but it is a bit of computer science jargon.

The word « algorithm » has a precise meaning. A well defined problem, with all the required inputs, which is decidable might have an algorithm to solve it. But some problems are very complicated and developers and researchers haven’t found an algorithm to solve this class of problem in a human time.

That is to say that an algorithm exists, but this very algorithm will find the solution only in a billion years. It might be a bit long to wait for such an algorithm to finish.

What kind of problems can be so complicated that we can’t create an algorithm to solve it in a human life time ?

The traveling salesman problem.

« Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city? »

It does not look so complicated after all ? Let’s try it.

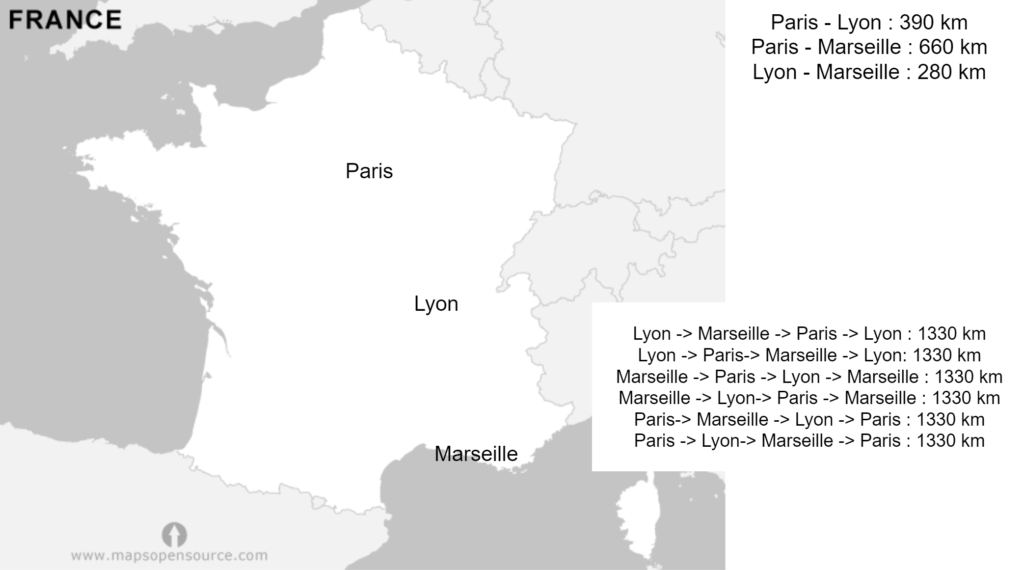
With 3 cities, it is not complicated, there is not a lot of possibilities and all possibilities are equals.

With 4 cities there are more possibilities. There are exactly 24 possibilities. So far, it is not very complicated for a computer or a smartphone to compute all possibilities and then outputs the optimal solution. As you can see, the solution is not unique.

Why is this problem a « very very very very very very hard » problem ? In computer science a problem complexity is not measured on small inputs. 4 cities is a small input. A problem complexity is studied when the input is very big, when the input size approaches the infinity. In this case no need to go that far. Let’s study this problem complexity.

The traveling salesman problem is known because its complexity is huge even with small input. Each time a city is added, the number of possibilities is multiplied by the city’s rank. It is a factorial. If « n » is the number of cities, the number of possible trips is factorial(n). Example: n = 5, trips = 1 x 2 x 3 x 4 x 5 = 120.

Number of cities	Number of possible trips
1	1
2	2
3	6
4	24
5	120
10	3 628 800
20	2 432 902 008 176 640 000
30	> 1033

If a computer can investigate 1000 possible trips per second, it needs 2 432 902 008 176 640 seconds to investigate all the possible trips for 20 cities. A year is 31 536 000 seconds so this computer needs 77.1 millions years to iterate through all the possibilities for only 20 cities.

For 30 cities it is roughly 1000 billion billion years: 1000 000 000 000 000 000 000 years. It is staggering!

On Earth there are roughly 2 billion computers – any kind of computer -. Let’s assume all these computers can explore 1000 trips per second each. So for 30 cities, we need 500 billion years to explore all the possible trips hence finding the shortest trip. I don’t even talk about all the required engineering to put this problem into so many computers.

But, we need to solve this problem even if we don’t get the optimal solution.

Acceptable heuristics

A heuristic is a program created to solve a problem but it finds the solution only most of the time. Sometimes the heuristic fails.

However when there is a very hard problem, a NP hard problem, and we desperately need a way to find a solution in an acceptable time, we are keen to accept a trade-off between the speed of the program and the optimal solution.

Many heuristics can yield very good results for the traveling salesman problem in a reasonable time and very close to the optimal solution.

Often heuristics start with a not optimized solution and try to improve it. This kind of algorithms are members of the the « genetics algorithms » family,

Conclusion

An algorithm can’t be weak or strong, an algorithm is not magic, an algorithm is just a program created to solve a well defined decidable problem in a human time or not. Too often heuristics are mistaken for algorithms, but the main difference between algorithms and heuristics is that heuristics can fail and output an incorrect solution.

A tremendous quantity of services people use daily are actually heuristics. Most of the time these heuristics succeed and sometimes fail, but systems are built so this can be an acceptable failure. Artificial vision, voice recognition, automatic translation, advertising, fraud detection, high frequency trading, machine learning for medical diagnosis, machine learning in social networks, machine learning in insurance, shortest path for GPS and so on.

Designing an algorithm can be complex, but the implementation is also something not to be neglected. Despite the algorithm correctness, the implementation can have flaws, hence the whole system is not doing exactly what we want.

After all, programs are coded by humans and they can be wonderful and terrible.